重庆大学第十五届校赛暨西南邀请赛决赛
2018-05-29
A.简单题
签到题,懒得写
B. Costly Graphs
NTT数学题,丢给队友,不补
C. The King’s Problem
缩点之后求最小路径覆盖
/*
* Author: JiangYu
* Created Time: 2018/5/29 1:22:22
* File Name: C.cpp
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define MP make_pair
#define PB push_back
#define X first
#define Y second
#define FI first
#define SE second
#define inf 0x3f3f3f3f
#define FOR(i,a,b) for(int i = a; i <= b; ++i)
#define FORD(i,a,b) for(int i = b; i >= a; --i)
#define ALL(x) x.begin(),x.end()
#define REP(i,a) for(int i = 0; i < a; ++i)
#define DEP(i,a) for(int i = a-1; i >= 0; --i)
#define CLR(a) memset(a, 0, sizeof a)
const int N = 10000;
int dfn[N],low[N],vis[N],Stack[N],color[N],du[N],cnt[N];
int n,m,top,sum,deep,tmp,ans;
vector<int> g[N], g2[N];
bool used[N];
int y[N];
void tarjan(int u) {
dfn[u] = low[u] = ++deep;
vis[u] = 1;
Stack[++top] = u;
int sz = g[u].size();
for(auto v : g[u]) {
if(!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
}
else {
if(vis[v])
low[u] = min(low[u], low[v]);
}
}
if(dfn[u] == low[u]) {
color[u] = ++sum;
vis[u] = 0;
while(Stack[top] != u) {
color[Stack[top]] = sum;
vis[Stack[top--]] = 0;
}
top--;
}
}
void init() {
CLR(vis), CLR(dfn), CLR(du);
CLR(low), CLR(cnt), CLR(color);
CLR(Stack), CLR(y);
sum = top = deep = tmp = 0;
}
bool path(int u) {
for(auto x : g2[u]) if(!used[x]) {
used[x] = 1;
if(y[x] == 0 || path(y[x])) {
y[x] = u;
return 1;
}
}
return 0;
}
int main() {
int t;scanf("%d", &t);
while(t--) {
scanf("%d%d", &n, &m);
init();
for(int i=1; i<=n; i++)
g[i].clear(), g2[i].clear();
for(int i=1; i<=m; i++) {
int from, to;
scanf("%d%d", &from, &to);
g[from].PB(to);
}
for(int i=1; i<=n; i++) {
if(!dfn[i]) {
tarjan(i);
}
}
for(int i = 1; i <= n; ++i) {
for(auto x: g[i]) if(color[i] != color[x])
g2[color[i]].PB(color[x]);
}
int num = 0;
//cout << sum;
for(int i = 1; i <= sum; ++i) {
CLR(used);
if(path(i)) num++;
}
printf("%d\n", sum - num);
}
}
D. 国家集训队论文集
统计有多少个相同的数字
签到题,代码懒得贴
E. OneDoubleC的小卡片
最小的放中间,大的放两边。最大的放中间,小的放两边。两种方式取最大。
/*
* Author: JiangYu
* Created Time: 2018/5/28 23:34:35
* File Name: E.cpp
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define MP make_pair
#define PB push_back
#define X first
#define Y second
#define FI first
#define SE second
#define inf 0x3f3f3f3f
#define FOR(i,a,b) for(int i = a; i <= b; ++i)
#define FORD(i,a,b) for(int i = b; i >= a; --i)
#define ALL(x) x.begin(),x.end()
#define REP(i,a) for(int i = 0; i < a; ++i)
#define DEP(i,a) for(int i = a-1; i >= 0; --i)
#define CLR(a) memset(a, 0, sizeof a)
int a[1024];
int b[10000];
int n;
bool cmp(const int o, const int t) {
return o > t;
}
int minsort() {
sort(a+1, a+1+n, cmp);
memset(b, 0, sizeof b);
int front = 1, flag = n-1;
int l = 5000, r = 5000;
b[5000] = a[n];
while(front <= flag) {
if(front > flag) break;
b[--l] = a[front++];
if(front > flag) break;
b[++r] = a[front++];
if(front > flag) break;
b[--l] = a[flag--];
if(front > flag) break;
b[++r] = a[flag--];
}
int ans = 0;
for(int i = l; i < r; ++i) {
ans += abs(b[i] - b[i+1]);
}
return ans;
}
int maxsort() {
sort(a+1, a+1+n);
memset(b, 0, sizeof b);
int front = 1, flag = n-1;
int l = 5000, r = 5000;
b[5000] = a[n];
while(front <= flag) {
if(front > flag) break;
b[--l] = a[front++];
if(front > flag) break;
b[++r] = a[front++];
if(front > flag) break;
b[--l] = a[flag--];
if(front > flag) break;
b[++r] = a[flag--];
}
int ans = 0;
for(int i = l; i < r; ++i) {
ans += abs(b[i] - b[i+1]);
}
return ans;
}
int main() {
int t;
scanf("%d", &t);
while(t--) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%d", &a[i]);
cout << max(minsort(), maxsort())<<endl;
}
return 0;
}
F. 任香香公主遇上女装群群主
垃圾题面,看了就不想写.
可以发现,从左上角走到右下角至少要$n+m-2$步,也就是说,我们从左上角出发,只能向下或者向右的路径上。
至多只能执行一次向上或者向左的走法。
我们先预处理出,从左上到右下只能向下向右走 与 从右下到左上只能向上向左走的两种情况。
画图发现想要将两种情况拼接起来,在不重复选的前提下,只有如下4种情况:
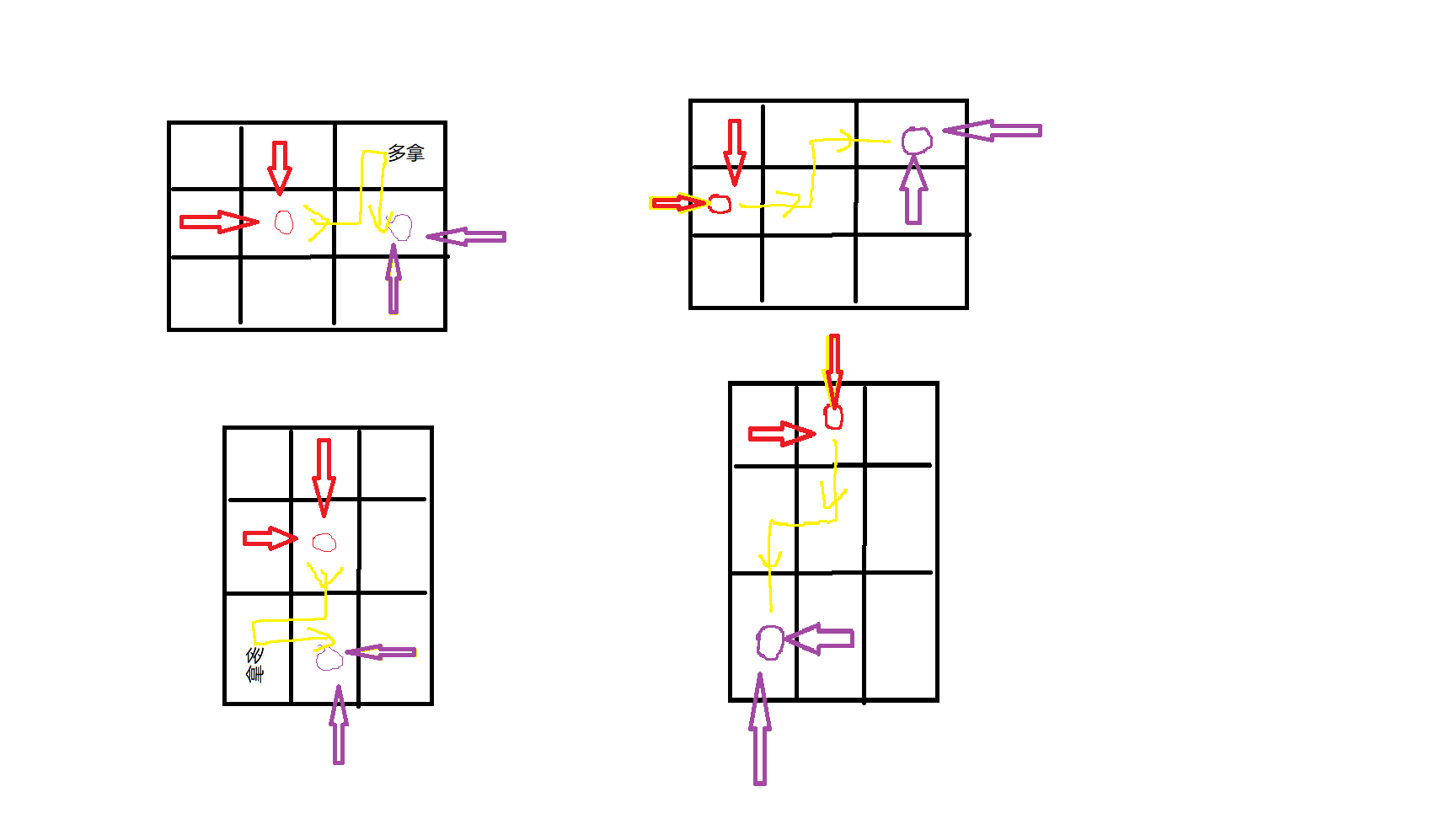
/*
* Author: JiangYu
* Created Time: 2018/5/28 23:58:34
* File Name: F.cpp
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define MP make_pair
#define PB push_back
#define X first
#define Y second
#define FI first
#define SE second
#define inf 0x3f3f3f3f
#define FOR(i,a,b) for(int i = a; i <= b; ++i)
#define FORD(i,a,b) for(int i = b; i >= a; --i)
#define ALL(x) x.begin(),x.end()
#define REP(i,a) for(int i = 0; i < a; ++i)
#define DEP(i,a) for(int i = a-1; i >= 0; --i)
#define CLR(a) memset(a, 0, sizeof a)
const int N = 1024;
int n, m;
int a[N][N], f[N][N], g[N][N];
int main() {
int t;
scanf("%d", &t);
while(t--) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]);
f[1][1] = a[1][1];
for(int i = 2; i <= n; ++i)
f[i][1] = f[i-1][1] + a[i][1];
for(int i = 2; i <= m; ++i)
f[1][i] = f[1][i-1] + a[1][i];
for(int i = 2; i <= n; ++i)
for(int j = 2; j <= m; ++j)
f[i][j] = a[i][j] + max(f[i-1][j], f[i][j-1]);
g[n][m] = a[n][m];
for(int i = n-1; i >= 1; --i)
g[i][m] = g[i+1][m] + a[i][m];
for(int i = m-1; i >= 1; --i)
g[n][i] = g[n][i+1] + a[n][i];
for(int i = n-1; i >= 1; --i)
for(int j = m-1; j >= 1; --j)
g[i][j] = a[i][j] + max(g[i+1][j], g[i][j+1]);
int ans = f[n][m];
//cout << ans<<endl;
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
if(j<=m-1&&i>=2)
ans = max(ans, f[i][j] + g[i][j+1] + a[i-1][j+1]);
if(i<=n-1&&j>=2)
ans = max(ans, f[i][j] + g[i+1][j] + a[i+1][j-1]);
if(j<=m-2&&i>=2)
ans = max(ans, f[i][j] + g[i-1][j+2] + a[i][j+1] + a[i-1][j+1]);
if(i<=n-2&&j>=2)
ans = max(ans, f[i][j] + g[i+2][j-1] + a[i+1][j] + a[i+1][j-1]);
}
}
printf("%d\n", ans);
}
return 0;
}
G. Boring Problem
先考虑如果只有一个询问,则可以通过贪心来计算至少开多少张发票。 即从右往左,累计和 < k 就都往这张发票上开,否则新开一张发票。
那么我们可以考虑用倍增来快速计算所有的询问,用fa[i][j]表示从第i个开始,$2^j$ 张发票能控制到的最左边的地方。 $fa[i][j] = fa[fa[i][j-1]][j-1]$,自己画一下就能理解了
/*
* Author: JiangYu
* Created Time: 2018/5/29 17:06:11
* File Name: g.cpp
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define MP make_pair
#define PB push_back
#define X first
#define Y second
#define FI first
#define SE second
#define inf 0x3f3f3f3f
#define FOR(i,a,b) for(int i = a; i <= b; ++i)
#define FORD(i,a,b) for(int i = b; i >= a; --i)
#define ALL(x) x.begin(),x.end()
#define REP(i,a) for(int i = 0; i < a; ++i)
#define DEP(i,a) for(int i = a-1; i >= 0; --i)
#define CLR(a) memset(a, 0, sizeof a)
const int N = 1e5 + 1024;
int n, K, q;
ll a[N], fa[N][20], sum[N];
int big[N];
ll get(ll x, ll y) {
return sum[y] - sum[x-1];
}
int main() {
int t; scanf("%d", &t);
while(t--) {
scanf("%d%d%d", &n, &K, &q);
for(int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]);
sum[i] = sum[i-1] + a[i];
}
fa[1][0] = 0;
for(int i = 1; i <= n; ++i) {
ll l = 1, r = i;
big[i] = big[i-1];
if(get(i, i) > K) {
big[i]++;
continue;
}
while(l <= r) {
int mid = l + r >> 1;
if(get(mid, i) <= K) r = mid - 1;
else l = mid + 1;
}
fa[i][0] = r;
}
int s = (int) ceil( log2(n));
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= s; ++j) {
fa[i][j] = fa[fa[i][j-1]][j-1];
}
}
while(q--) {
ll x, y;
scanf("%lld%lld", &x, &y);
if(big[y] - big[x-1] > 0) {
puts("-1");
continue;
}
ll ans=0;
for(int j = s; j >= 0; j--)
if(fa[y][j] >= x)
ans += (1<<j), y = fa[y][j];
printf("%lld\n",ans+1);
}
}
return 0;
}
H. 课上例题和课后习题
矩阵快速幂,数学渣渣推不出系数,依旧丢给队友。
I. 完美主义人工智能AlphaOneDoubleC
所谓的 ‘合法序列’ ,意思是序列在从左往右的过程中任意时刻$S$数量不小于$A$数量。 利用这个性质:我们不妨将所有的问号都先置为’A’,再从左往右将’A’变为’S’,使得序列合法, 每次的选择都是保证当前0~i段序列合法的最小花费,当i等于序列长度时也成立。
/*
* Author: JiangYu
* Created Time: 2018/5/29 19:58:19
* File Name: I.cpp
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define MP make_pair
#define PB push_back
#define X first
#define Y second
#define FI first
#define SE second
#define inf 0x3f3f3f3f
#define FOR(i,a,b) for(int i = a; i <= b; ++i)
#define FORD(i,a,b) for(int i = b; i >= a; --i)
#define ALL(x) x.begin(),x.end()
#define REP(i,a) for(int i = 0; i < a; ++i)
#define DEP(i,a) for(int i = a-1; i >= 0; --i)
#define CLR(a) memset(a, 0, sizeof a)
const int N = 1e5 + 1024;
typedef pair<ll, int> PI;
priority_queue<PI> que;
char ch[N];
int n, k, num;
ll sum;
bool flag;
int main() {
//freopen("2.in", "r", stdin);
int t; scanf("%d", &t);
while(t--) {
scanf("%d%d", &n, &k);
scanf("%s", ch);
flag = 0;
sum = 0;
num = 0;
for(int i = 0; i < 2*n; ++i) {
if(ch[i] == 'S') num++;
else if(ch[i] == 'A') num--;
else {
int a, b;
scanf("%d%d", &a, &b);
sum += 1ll* b;
num--;
que.push(PI(1ll*(b-a), i));
}
if(num < 0) {
if(que.empty()) {
flag = 1;
continue;
}
PI front = que.top();
que.pop();
sum -= front.first;
num += 2;
}
}
if(num != 0 || flag == 1) puts("-1");
else
printf("%lld\n", sum);
while(!que.empty()) que.pop();
}
return 0;
}